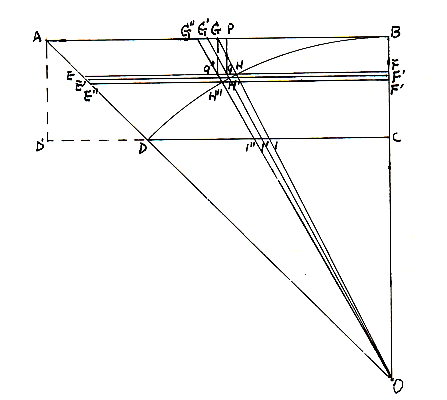
解:右图△AOB为ʘ0

外切正方形的，BO

为半径，B为切点，G为AB

中点，GO与BD交于H点，

EF过H点平行于AB，Pq过

GH中点，垂直于EF，q点为垂足

G’0过q点与BD相交于H’点,E'F'过

H'点平行于EF，E'F'则为与ʘ0面积相等

正方形边长的，（图中含证题作图）。

证明：

1、简介：图中梯形ABCD简称梯形，梯形内圆以外部分称弧外，圆以内部分称弧内，以r为半径弧外面积，弧内面积为，弧内外面积差称为1个内外差，弧外小于梯形个内外差，弧内大于梯形个内外差，等分AB的点与0点的连线等分△A0B，也等分梯形，这样的等分线在梯形内的部分称为梯形的径线，过径线与BD的交点作线段平行AB抵梯形的两腰，这样的线段称为径线的对应线段，两条相邻径线间的面积称为单条径线面积，单条径线面积不变，单条径线面积可以组成梯形内任意径线面积，对应线段面积与径线面积必须同含BD的同1个弧段，单条径线面积相对单条对应线段面积，两种面积分别组成梯形面积。

2、单条对应线段面积自上而下，由小到大：根据△AOB角之间关系可知△AOB等分线之间圆心角逆时针方向由大到小，所对弧长也由大到小，也是径线间弧长从B点往D点由大到小。

∵ B为切点，径线间弧段越长则越近B点，越近B点弧段端点垂直间距越小，越近D点则与B点相反，弧段端点垂直间距越大。

∴ 径线间弧段端点垂直间距从B点到D点由小到大。

∵ 单条对应线段面积与单条径线面积含同一个弧段，单条对应线段面积为1个小梯形。其所含弧段端点垂直间距为面积小梯形的高。    

∴ 单条对应线段面积小梯形的高从上而下由小到大。

∵ AB与其相邻的1条对应线段两者组成的单条对应线段面积，如果对应线段无限接近AB其面积趋于0，高也趋于0，而对应线段为最长。

∴ 这1例说明单条对应线段面积与对应线段长度成反比，与对应线段面积小梯形的高成正比。

∵ 图中D'D为CD延长线，△AD'D为等腰直角三角形，AD'=D'D，AD'为全部对应段面积小梯形的高之和，D'D为全部对应线段递减之和，两个和相等，说明整个梯形高主导单条对应线段面积，因而单条对应线段面积与面积小梯形的高成正比，与对应线段长度成反比成立。

∴ 单条对应线段面积自上而下,由小到大。

3、如果径线 G'I'左部与弧外相等，右部与弧内相等，则对应线段E'F'上部与弧外相等，下部与弧内相等：根据弧内外径线占比可知弧外重心偏左，弧内重心偏右，如果两者分别整合成径线面积，则梯形左部为弧外，右部为弧内，设分界径线G'I'。

∵ G'I'左部为弧外，右部为弧内，则G'BH'=DH'I'。

 这两个相等面积以外，弧内外的其余部分仍保持弧内外的1个内外差，在G'I'径线上的G'H'对应弧外部分，H'I'对应弧内部分，如果G'H'与H'I'的长度比例改变，则两者分别对应的弧内外就不为1个内外差，就不能分别代表标准的弧外和弧内。

∴ G'H'与H'I'的长度比等于弧外与弧内面积比。

∵ G'H'与H'I'的长度比等于弧外与弧内面积比。

∴ 过H'点的G'I'的对应线段E'F'上部与弧外面积相等下部与弧内面积相等。

∵ E'F'下部与弧内面积相等，则 E'F'为所求正方形边长的。

∴ 只要证明G'I'位置就达到证题目的。

∵ 径线面积与对应线段面积含BD的同一弧段。

∴ G'1'右部径线面积对应E'F'上部对应线段面积，为弧内对应弧外，G'I'左部径线面积对应E'F'下部对应线段面积，为弧外对应弧内。

∵ 两种面积差=径线面积-对应线段面积

∴ 上述右上对应为弧内-弧外=1个内外差，左下对应为弧外-弧内=-1个内外差。

∵ 梯形的径线面积与对应线段面积相等，两种面积差为零。

∴ 以上必然1个内外差为正，1个内外差为负。

∵ 证3证明单条对应线段面积自上而下由小到大。而单条径线面积不变。

∴ 单条对应线段面积小于单条径线面积的部分在E'F'上部，而大于单条径线面积的部分在E'F'下部，E'F'上部与之相邻的1个单条对应线段面积在E'F'线段上与单条径线面积相等。

∵ 径线面积有正负两种面积差，其表示形式必然不同。

∴ 根据证题在正差范围，故不探讨负差内容。

4、外径线正投影三角形中，外径线对应径线面积，外径线左面正投影对应对应线段面积，外径线下面正投影对应两种面积差。

    每1条径线都有1个外径线正投影三角形，外径线为斜边，外径线左面正投影与下面正投影分别为直角边，如图中△Gq'H为径线GI的外径线正投影三角形，GH为外径线，Gq'为GH左面正投影，q'H为GH下面正投影。

∵ 每1条径线都分弧内外部分，径线处于弧外的部分称为外径线。从与BC相邻的1条径线的外径线为1个点到最终的外径线AD与1条径线相等，外径线的增长与径线面积增长同步。

∴ 每1个位置的外径线对应1个径线面积。

∵ 外径线左面正投影为对应线段面积小梯形（为区别梯形加小字）的高，高与小梯形面积成正比。

∴ 外径线左面正投影对应对应线段面积。

∵ 径线面积与对应线段面积为因果关系，外径线与其左面正投影分别对应径线面积和对应线段面积，两条线段也对应了因果关系。

∴ 外径线与其左面正投影分别对应径线面积和对应线段面积符合对应关系。

∵  两种面积差关系:对应线段面积+两种面积差=径线面积与直角三角形面积关系式为同一模式，在外径线正投影直角三角形中，径线面积对应斜边，对应线段面积对应外径线左面正投影直角边。

∴ 外径线下面正投影必然对应两种面积差。

∵ 在正差范围对应线段面积小于径线面积，如将两种面积补平则在对应线段面积下面补上了两种面积差，由于对应线段面积必有径线面积，按两种面积同一个弧段的要求，对应线段面积上的差对应的径线面积上的差必在径线面积左侧过外径线下面正投影，在图中举例为GI径线面积在其与BC之间，对应线段面积在EF与AB之间，补差对应线段面积在EF与E''F''之间，差的径线面积在G''I''与GI之间，过外径线下面正投影为q'H。

∴ 上述证明验证了外径线下面正投影对应两种面积差的正确性。

5、平分梯形面积的径线GI的两种面积差，其差的径线面积为1个内外差。

∵ 已知梯形大于弧外，小于弧内均为个内外差。

∴ DHI大于GBH 个内外差。

∵ 证3已知 DH'I'=G'BH'，可以认为是 DHI与GBH分别减少和增加两者面积差的而来，从图上看出这个增减在G'I'与GI之间，其弧内减少的面积就是弧外增加的面积。

∴ G'I'与GI之间弧内外均为 个内外差。

∵ DHI大于GBH 个内外差可以用假设径线G''I''与GI之间弧内面积为 个内外差来表示，而已知G'I'与GI之间弧内为 个内外差。

∴ G''I''与GI之间弧内 个内外差被G'I'等分，G''I''与G'I'弧内为 个内外差。

∵ G'I'与GI之间和G''I''与G'I'之间都可以看作两个不等面积变化为相等面积的过渡，都是弧内外面积增减相等。

∴ G''I''与G'I'之间弧内为 个内外差，弧外一定为个内外差，这样G'I'与GI之间为 个内外差，G''I''与G'I'之间也为个内外差，两部分均为弧内外面积相等。

∵ G'I'与E'F'为两种面积差正负差界线，G'I'两侧弧内外面积对等，说明BD在 G'I'两侧走向在均等面积之间，而产生两部分两种面积差均等变化的效果。

∴ G''I''与G'I'和G'I'与GI之间两种面积差均为个内外差的两种面积差，但方向相反。

∵ GI平分梯形，GI的径线面积处于GI与BC之间，与G'I'的径线面积与弧内面积相等对比差为个内外差，即G'I'与GI之间个内外差为GI径线面积比G'I'径线面积所小的面积。

∴ GI的两种面积差小于G'I'的两种面积差为G'I'与GI之间个内外差的两种面积差，因证3已知G'I'的两种面积差为1个内外差，故GI的两种面积可用1个内外差减个内外差的两种面积差表示。

∵ 按证4证明的两种面积差对应位置，G'I'与GI之间个内外差及其对应线段面积处于GI的两种面积差对应位置，也是前所证明的G''I''与GI之间1个内外差被G'I'等分的正差部分。

∴ 根据GI两种面积差的定义，GI两种面积差的对应线段面积按正差模式为个内外差加EF与E'F'之间面积即1个内外差减 个内外差的两种面积差。

∵ 上述与EF和E'F'之间面积相加的 个内外差处于负差范围，为之前所证明的G''I''与G'I'之间为个内外差的对应线段面积位置范围。

∴ 用正差模式理解，这个加上的个内外差的对应线段面积必然对应线段条数与G''I''和G'I'之间径线条数相等，面积相等。

∵ 在负差范围这个面积自然要扩大 个内外差的两种面积差，这个面积扩大是由径线位置所致，径线面积不会改变。

∴ GI的两种面积差的径线面积为G''I''与GI之间的1个内外差。（证题不需确定对应线段面积）

证毕。

参考文献

[1]张希仓.“化圆为方”问题[J].初中生世界,2023,(Z5):82.

[2]黄正洪.化圆为方及立方倍积的尺规思考[J].数学学习与研究,2020,(03):151.

[3]吴建军,刘晶.浅谈化圆为方问题的“前世今生”[J].求知导刊,2019,(32):5-7.DOI:10.14161/j.cnki.qzdk.2019.32.004