数学核心素养是学生在学习过程逐渐形成和发展起来的。数学练习则是核心素养形成的重要依托。通过练习，可以帮助学生理解和掌握数学的基础知识与技能，感悟和运用数学的基本思想与方法，获得数学的基本活动经验，让学生形成良好的学习习惯，积极的情感、态度和价值观，在数学学习过程中逐渐形成数学核心素养。在教学中，数学练习的设计应注重知识与方法的层次性、多样性，精准有效的练习设计方能达到事半功倍的效果。在平时的数学课堂教学中，一个单元的知识往往是分解成若干课时，再在每个课时中落实一个个小目标，从而完成单元教学；但在单元练习时，我们往往会发现教学效果不尽人意，这是什么原因呢？因为课时教学是将单元知识进行了相应的分解。这样的知识分解，更有利于突出重点、突破难点、提高课堂教学效率；但同时也有一些不足。如：课时教学中知识分解过度，比较关注知识的局部与细节，使学生缺乏对知识的整体性把握。笔者认为，在数学教学中如果注重练习整合，则可以弥补“知识孤立”这一不足。下面我将立足整体，以生为本，以“圆的练习设计”为例，探讨如何进行结构化练习整合，将核心素养渗透于练习中。

一、基础练习，复习基本技能方法；

    基础练习是对已学知识技能等的记忆重现，或在简单情景中加以应用。基础类练习要少而精，这类练习在形式和内容上最好能引起学生的学习兴趣，促进学生对数学核心知识和方法的理解与掌握，进而促进学生的发展。如《圆的面积》教学，在学生经历圆的面积计算公式探究，理解算理、掌握的算法的基础上，可以设计这样一组基础练习来巩固本节课的知识：

1.在公园的草地上，有一个自动旋转喷灌装置的射程是10 m，请你算一算：它能喷灌的最大面积是多少？

此题是基本圆的面积计算，只要学生结合生活实际理解 “射程”即是“半径”，喷灌的最大面积就是圆的面积（如图），便可以顺利解决这个问题。

2. 将一个圆剪拼成一个近似的长方形(如图），这个长方形的周长比圆的周长多8厘米，那么这个圆的面积是（       ）平方厘米。

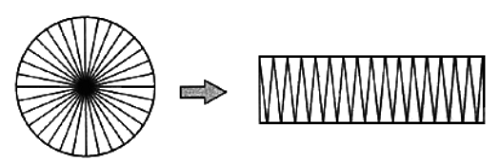
此题需将圆的周长与面积知识相结合，思考为什么“这个长方形的周长比圆的周长多8厘米”？继而回忆探究圆周长时“化曲为直”的方法，即多出的8厘米就是长方形的两个宽也就是圆的一个直径，那么一个宽就是圆的半径，知道圆的半径是4厘米，问题就迎刃而解了。

3.如图所示,圆的周长是18.84厘米,圆的面积与长方形的面积正好相等.图中阴影部分的面积是（    ），周长是（      ）。

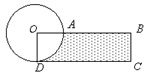
此题中，“圆的面积与长方形的面积正好相等”，说明就是用了面积探究中的切割术，将圆转换成长方形。因此可以根据圆的周长算出半径，再根据半径得出圆的面积，这个推理并不难；但是阴影部分的面积和周长与圆的面积和周长有怎样的联系呢？需要学生结合图，仔细观察，发现阴影部分的周长是圆周长的1倍，是圆面积的，这样既复习巩固了基本的计算方法，又沟通了知识之间的内在联系，让学生不仅知其然，更知其所以然。

二、对比练习，打通知识内在联系；

数学练习不是孤立存在的，每课时的练习都是相关联的，有前后递进关系，一些复杂的问题涉及综合运用需要适当的整合，可以沟通知识的联系与区别，帮助学生加深对所学知识内在联系的认识，完善知识结构，从而提高学生思维品质，发展核心素养。还可以设计这样的对比练习：

有一个长8厘米，宽5厘米的长方形，

（1）如果在里面画一个最大的圆，这个圆的面积是（   ），周长是（）；

（2）如果在里面画一个最大的半圆，这个半圆的面积是（  ），周长是（）。

此题（1）问中，学生往往会受“最大”这个词的影响，想到直径最大是8厘米，这个圆的直径可以是8厘米吗？这是学生解决这个问题的“模糊点”。当然，可以先让学生主动尝试，在模糊处允许学生正常犯错，再由学生纠正错误，说明错因：同一个圆内的半径是相等的，不能只考虑长的数量，在这里最大圆的直径是5厘米（如图1）。如果就题讲题到此为止，就错失了它更大的数学价值，因此增加了（2）问，因为有前一小题的思维引领，学生思路会顺畅很多（如图2）。最后将两个问题进行对比，学生会发现在解决问题时要多角度、全方位、综合考虑。另外，计算“一个圆”的周长还是“半个圆”的周长也是审题的重点，半圆的周长是圆周长的一半加直径更是易错点，这样的对比练习将所学知识的重点、难点、易错点融会贯通，更有利于打通知识之间的内在联系，完善知识结构，同时有利于对学生思维的深刻性、逆向性、批判性的指导和渗透，提高学生思维品质，发展核心素养。

    （图1）                    （图2）

三、变式练习，贯通知识本质属性；

数学学科中最富有生命力、最具有统摄力的是数学观和数学方法论，即数学思想。在练习设计时，应重视和加强数学思想的教学，才有利于贯通知识的本质属性，让学生掌握思维方法，促进思维发展。如在扇形面积教学后，可以安排这样一组练习：

（1） 基本题1：（如图）有3个完全一样的圆，面积都是80平方分米，求阴影部分的面积。

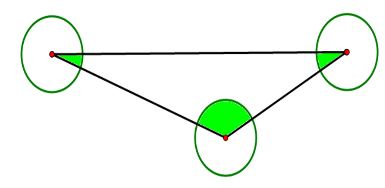
      （提示：阴影部分是半个圆的面积。因为三角形内角和是180°。）

（2） 基本题2：（如图）有4个完全一样的圆，面积都是80平方分米，求阴影部分的面积.

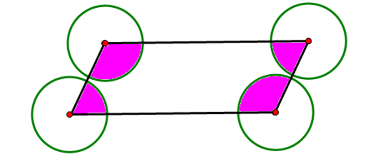
（提示：阴影部分面积是一个圆的面积。因为四边形内角和是360°，或者可以把四边形分成两个三角形，180+180=360°。）

（3） 变式题（如图）有5个完全一样的圆，面积都是80平方分米，求阴影部分的面积。

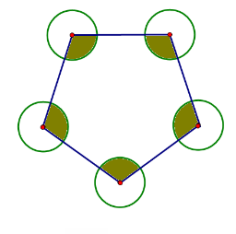
（提示：阴影部分面积=一个圆的面积+半个圆的面积，引导学生可以用分割三角形的方法，也可以试着动手剪拼。）

这样一组变式练习，让学生在观察、比较、思考的过程中感受到这类题目的内涵：圆心角的度数是决定面积大小的根本因素，而圆心角的度数就是多边形内角和度数。这样的练习，让学生更容易把握知识的本质属性，同时也充分挖掘了习题的思维价值，让学生收获了心智的启迪和经验的唤醒。

四、拓展延伸，培养学生迁移能力。

拓展延伸练习是对课堂学习的进一步拓展与深化，基于学习情景，突出课程育人功能，强调在一块知识中形成迁移应用能力。拓展延伸能有效地突破重点、化解难点，让学生获得学习方法、解题策略和数学思想。有些练习如果仔细分析，用好用活能发挥更大的价值。如：

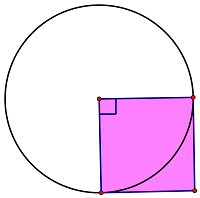
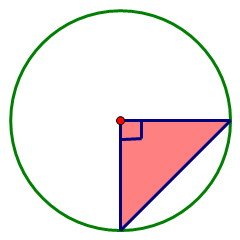
1. 已知正方形面积是10平方厘米， 2. 已知三角形面积是10平方厘米，

求圆的面积。                     求圆的面积。

3.已知阴影部分面积是50平方厘米， 4.已知阴影部分的面积是50平方

求圆环面积。                    厘米，求圆环面积。

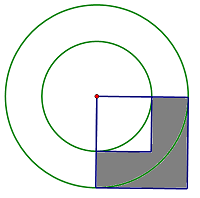
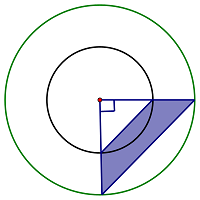
   这是在圆的面积单元教学后设计的一组拓展延伸题。学生的发展是建立在对基础知识完全理解和掌握的基础上的，练习设计要注重以各种方式将旧知识重新包装起来，提高学生练习兴趣，促进学生积极思考。这组题中1题是基础题，比已知半径算起来还要方便，因为半径的平方是已知的，只要一步计算即可；有了1题的启发，可以把学生带进“最近发展区”，而后面3题的拓展延伸则是落实并加速“最近发展区”的发展。尤其是第4题，大部分学生寻找、计算（R²-r²）时可能存在困难，但问题是思考的动力和方向，随着思考的深入，学生通过观察、猜测、推理、验证等方法仍然可以发现“50乘2”就是（R²-r²），学生对这类知识的认识和理解逐渐深刻。

拓展延伸的练习对学生要求较高，有时根据需要可以利用多媒体手段辅助教学，为学生提供丰富、直观的学习资源，这类题目可以点燃学生主动探究的热情，帮助学生建立空间模型，激发他们的想象力，从而提高学生的数学素养。

总之，练习为学生提供了新的学习机会，使学习再发生；练习为教师了解学生打开了一扇窗，使教学更有效。教师要不断探索，从学生实际情况出发，注重练习整合，突破“见树不见林”的课时思维，精心设计练习，注重练习整合，方能促进学生核心素养的培育。

参考文献：

[1]余文森.小学数学:名师高效教学设计艺术[M].西南师范大学出版社,2010.

[2]阮祥燕.小学数学单元作业的设计与实施[J].基础教育研究,2021(13):69-70.

[3]吕娜,芮志成.“双减”背景下小学数学减负增效的实践与思考[J].教学与管理,2022(14):47-51.

[4]贾福录.设计体现核心素养的基础性作业[J].小学数学教师,2022(05):55-58.