2022年版的《义务教育数学课程标准》中明确指出：数学是研究数量关系和空间形式的科学，数学素养是现代社会每一个公民应该具备的基本素养^[]。并提出了在数学课程中，应当注重发展学生的数感、量感、符号意识、空间观念、几何直观、数据分析观念、运算能力、推理能力和模型思想。而这些核心素养的落实，离不开“数”和“形”。可以说，数形结合思想的渗透是发展学生数学核心素养的基础，是数学学科教学的本质。

为了解目前数形结合思想在小学数学教学中的应用情况，笔者制定了教师和学生问卷，对区域内十所学校的师生进行调查，收到有效学生问卷1605份，有效教师问卷105份。经统计分析发现：98.1％的学生觉得数形结合思想有助于理解题意，但是经常运用图形解决问题的却只有21.25％的学生；72.38％的教师认为非常有必要在小学数学教学中渗透数形结合思想，但是只有29％的教师知道自己所任教的教材中哪些知识可以渗透数形结合思想，54.29％的教师在提到数形结合时几乎等同于直观教学，75.64%的教师把数形结合当做一个解题方法，并没有作为一个数学思想在教学中有意识地进行渗透。笔者通过长时间的实践和总结，认为可以从以下几个方面来渗透数形结合思想。

一、在数与代数的教学中，以形助数，提高数学素养

（一）以形助“数的认识”，培养数感

在小学阶段，学生先后认识的数有自然数、分数、小数、百分数、负数等，如下表一，这些构成了小学阶段“数”的知识体系，但是这些知识是抽象的，不利于学生理解。这就需要教师借助图形来帮助学生理解数的概念，只有达到理解的程度，才能让学生建立对数的感觉，也就是达到培养数感的目的。

表一  人教版教材关于数的教学在各年级的分布

例如：在教学《认识几分之一》这一节课，教师先结合具体情境“分月饼”，通过直观图形，让学生初步感受月饼的指的是什么，紧接着通过“折一折”、“画一画”正方形的，“辩一辩”下面哪些图形表示的是（如图一），通过这些活动，让学生充分感知“二分之一”的意义，初步建立“二分之一”的模型，为进一步学习其他分数做好铺垫。整节课的教学都离不开图形，通过图形，把抽象的分数意义直观化，达到认识概念本质的目的。在这个过程中，学生经历了认识分数的活动过程，逐步积累数感经验。

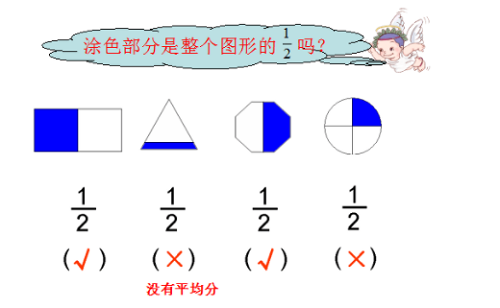
图1

（二）以形助“数的运算”，感悟算理

四则运算和运算定律意义的理解是“数的运算”的基础。在教学中，要求学生掌握一定的计算技能，这是学好数学的关键。而计算技能的培养，除了要让学生掌握计算方法，更要让学生理解算理。“算理”对于学生来说是抽象的、复杂的，这就需要教师通过“以形助数”，渗透数形结合思想，达到感悟算理的目的。

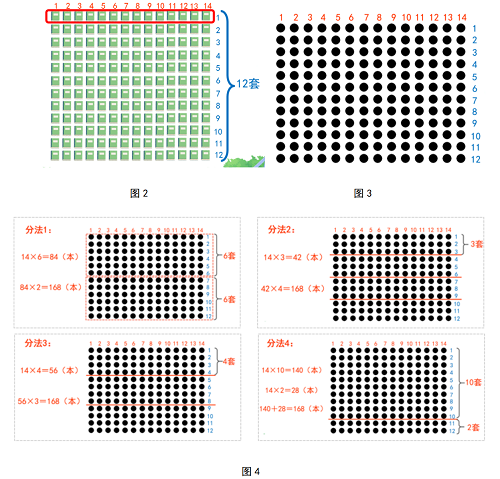
例如：在教学《两位数乘两位数笔算乘法》时，先提出问题情境“每套书有14本，王老师买了12套。一共买了多少本？”为了帮助学生理解题意，教师提出可以画图。就得到了图2，因为数学简洁、具有高度概括性的特点，在教师的引导性，学生想到用点子图（图3）来表示，这是一个去外在、符号化的过程。

接着就是计算了，因为“两位数乘两位数”学生以前没有学过，所以他们在图中圈一圈、算一算，共想到4种算法，如图4，把新知转化成旧知。总结这四种算法，学生发现相同点都是先分后合，而不同点是前三种是平均分，最后一种是分成整十和一位数，这种最简单，也更具有普遍性，它其实就是两位数乘两位数笔算的算理。通过这样的活动，学生从形的方面具体思考逐步过渡到数的方面进行思维，不仅可以较为深刻地理解算理，同时促进了形象思维和逻辑思维的协调发展。

二、在图形与几何教学中，以数辅形，提高数学素养

通过调查，笔者发现54.29％的数学教师在提到数形结合时几乎等同于直观教学，他们只重视以形助数，而忽略以数辅形。我国著名数学家华罗庚曾说过：“数缺形时少直观，形少数时难入微，数形结合百般好,隔离分家万事休”。可见，数和形各具优点，“数”侧重于抽象的逻辑思维，“形”则偏向于形象思维，数形结合将数量关系与空间形式密切联系、巧妙结合，有利于学生对数学知识概念的理解，也体现了哲学上联系整合的思想。所以，培养数形结合思想，既要做到“以形助数”，还要做到“以数辅形”，不可夸大某一方面的作用，要从整体上把握，使二者相辅相成。

例如：在学生理解了什么是“面积”的概念之后，出示了大小相近的一个长方形和一个正方形，那么长方形面积大还是正方形面积大呢？这时就需要学生用数来刻画，体现了“数”的准确性、规范性、严密性。

例如:在比较周长和面积时，教师设计了这样一个环节：用16米栅栏围一块长方形或正方形地，怎样围面积最大（长和宽都是整米），这虽然也是“形”的问题，但通过“形”学生并不能确定怎么围面积最大。这时就需要教师引导学生通过填写下表（表二），利用“数”的计算来使学生理解“周长相等时，长、宽之差越小，所得的长方形面积越大”这个规律。

表二

学生经过研究得到：长7米、宽1米；长6米、宽2米；长5米、宽3米；长4米、宽4米（正方形），这四种情况，其中正方形的面积最大。通过这样的研究，学生会发现：要想得到最大的面积，就需要把各种情况列举出来，再比较；在周长不变的情况下，需要改变长和宽的大小，长逐渐增加，宽就随之不断减小。这样就把“静态”的学习变成了“动态”的研究，这种由“静”到“动”正是函数的本质^[]。通过“数”的研究使学生对周长和面积及其关系有更加理性、深入的认识，是“以数辅形”很好的体现

三、在解决问题中，数形结合，提高数学素养

数学教育既要培养学生数学知识和技能，更要培养学生的数学思维能力和创新能力。而这些能力的培养，离不开“数”和“形”。教学“数”的问题时，教师可以引导学生充分利用直观的“形”把抽象的数量关系具体表示出来，使复杂的数学问题直观化；教学“形”的问题时，教师可以引导学生充分利用“数”的准确性、规范性、严密性，阐明形的某些属性。除了在新课教学时，要像这样渗透数形结合思想，在解决实际问题时，也要注意数形结合思想的渗透，从而提高学生解决问题的能力，提高学生数学素养。

例如：生活中常见的和差问题：“两筐水果共重150千克，第一框比第二框少10千克，两筐各重多少千克？”这个问题对于小学生来说比较复杂，有的教师在教时，让孩子记住公式“（和+差）÷2=大数  和-大数=小数”或者“（和-差）÷2=小数  和-小数=大数”，学生背的滚瓜烂熟，但是一问到原因，学生就答不上来了。其实这一题，引导学生画线段图（如图5），通过线段图直观描述数量之间的关系，学生很容易理解：150千克加上10千克，就是2个第二框的重量，150千克减去10千克就是2个第一框的重量。学生在这样的过程中切实感受到画图的重要作用，进而培养了数形结合的思想，提高他们解决问题的能力。

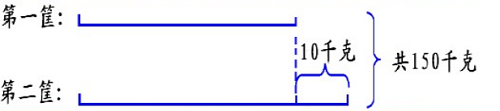
图5

综上所述，数形结合思想是解决数学问题重要的方法和思想，是学生学好数学的前提，所以作为数学教师，首先要意识到数形结合思想的重要性，这样才能在平时的课堂教学中有意识地去渗透数形结合思想。从“以形助数”和“以数辅形”两方面展开新课教学，同时在解决实际问题时，有意识地渗透数形结合思想。长此以往，学生的形象思维和抽象思维都能得到发展，学生能用数学的眼光观察世界，能用数学的思维思考现实世界，数学素养得以提高。