转化思想在初中数学解题中的应用可以使原本枯燥无味的数学知识变得更加形象直观化，同时也会使我们更加深刻地理解所学知识。使学生在遇到具体题目时不会感到无从下手，而是可以在脑海中大致确定解法和思路，并能够利用自己所掌握的知识去将其进行灵活的运用。在初中数学解题中，转化思想的应用是十分重要的，它不仅可以帮助我们解决在数学解题中遇到的难题，还可以培养我们的发散思维，更好地运用数学知识与方法解决实际问题。也可以是运用类比、联想等方法来深化理解；还可以是将数学问题通过转化思维方式来解决等。

一、转化思想概述

数学学科由于自身的特点表现出非常强的逻辑关系，推理论证要环环相扣。为此，解题时需要结合数学已有的知识对复杂问题进行分析，通过数学方法将其变形，成为易于分析和解决的问题，这种转化的方式，又被称作为转化思想。同时，转化的本质则是对问题之间存有的联系进行揭示，对数学问题进行转化，除了较为简单的问题外，大多数的数学问题都可以运用转化思想实现问题的有效解答。因此，转化思想作为问题解决的主要思想，其解题的过程通常就是转化的过程。在数学解题中，教师就需注重转化思想的运用，如间接转化、类比转化、数形结合等都是转化思想的表现，因地制宜引导学生依据试题的特点和规律，采用适合的方法进行转化，将未知、抽象和复杂的问题转化为已知、简单和具体的一个或几个问题，这样，学生就能够将复杂问题与已有知识联系起来，并运用数学的方法有效解决问题。

二、转化思想的应用

（一）间接转化，化复杂为简单

间接转化的运用主要是对较为复杂的数学问题进行解决，较为常见的有换元法，在几何图当中画反推或辅助线，或设未知数x，都属于间接的转化形式。初中阶段的学生在对数学问题进行解答中，通常会出现无法解决的情况。数学间接转化也可以把数学问题的整体分解成不同的小问题，其主要目的就是对综合性数学题的解答中，通过加减乘除的运算以及因式分解，把繁多条件的几何问题实施相应的分解转化。经过该方式，不仅能实现数学题目的简化，而且还能实现解题效率的提高。通常来说，数学教材当中有许多复杂的题型，主要是多种题型堆叠、变形、交互形成的。初中生在对复杂的数学问题进行解答中，通常会遇到题型比较复杂数学题，这就会使学生在解题时出现相应的抵触情绪，认为自己无法解答相关数学题。面对这种状况，数学教师就需注重引导学生运用转化思想实施解题，并让学生以平和的心态面对复杂的数学题，对数学题目进行仔细阅读，对数学题当中的意志条件进行认真分析，并通过转化思想实施解题，从而使复杂的数学题实现简单化。例如，求方程

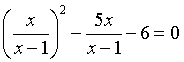
解。对于初中生来说，开平方以后，问题会变得异常复杂，因此可以观察方程，令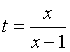，则原方程转化为t²－5t－6＝0，即（t＋1）（t－6）＝0，t＝－1，或t＝6，将其带入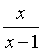，可得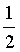，x＝，或x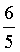＝。通过这种方式，有效降低可数学题的复杂度，而将复杂的数学题转成简单的数学题，有助于学生对数学题的分析，而且还能使学生解题的自信心得到有效提高。

（二）类比转化，化抽象为直观

初中数学解题中，可把分数加减乘除各种运算转化成分式加减乘除的运算，该过程中，需注重运算符号的先后顺序，并间接性进行转化。学生在解决数学问题时，通过类比转化，促使抽象内容转化为形象内容，以发现其相同与不同的点，确保解题的正确性。初中阶段的数学问题与小学阶段相比，其明显的不同是问题越来越抽象，面对刚步入初中的学生而言，其通常无法有效适应数学题的解答。基于此，数学教师在解题教学时，就需注重指导学生把抽象问题转变成直观问题，以帮助学生更好地解决相关数学问题。使数学问题直观化，其不仅有助于学生解决初中阶段的数学问题，而且还能使学生无法解答的抽象问题实现具象化、直观化，从而使学生更好地理解与解决相关数学问题，并使学生自身的转化思维、逻辑思维及其应用能力得到有效增强，最终促进学生在数学解题中的解题能力提高。例如，已知，m²＋6m－3＝0，n²＋6n－3＝0，其中m≠n，求：mn＋3m＋3n的值。就初中生而言，本题的求解极其抽象，学生无法在题目当中找出具体的解题思路。通过观察方程的形式，其类似一元二次方程，并且m≠n，则可以类比一元二次方程x²＋6x－3＝0的两个根，然后依据根与系数的关系可得：m＋n＝－6，mn＝－3，则mn＋3m＋3n＝mn＋3（m＋n）＝－21。这样，就把抽象的数学问题通过类比转化为已知的知识，使学生形象地理解相关数学问题，运用已经掌握的知识和方法解决问题，从而得出正确答案。

（三）数形转化，数与形互助

数形转化属于较为常见的一种转化方式，在解决实际问题时，需结合问题条件，实现代数与图形之间的互相转化，通过数形来更好地体现知识本质，为学生解题提供思路，就是数形转化。数形转化包含以形助数和以数辅形两个方面，主要是在具体的数学课堂教学或问题分析中，以数学问题作为出发点，明确数学题目中所隐藏的数量关系，借助“数”和“形”之间的相互转化，将复杂、抽象的问题简单化、具体化，进而使得初中数学知识点直观、形象地呈现在学生的面前。数形转化能够揭示数学的本质规律，体现出“数”与“形”之间的关系，能够避免大量的分析和计算过程，提高解题效率。例如，小明一共有500元钱，已知故事书的价格是60元每本，漫画书的价格是70元每本，小明计划用500元钱买故事书和漫画书，其中故事书不少于3本，漫画书不少于2本，那么，小明一共可以有多少种购买方式可以选择？如果学生用枚举法，过程复杂，也容易发生遗漏，而通过数形转化，将代数问题化为图形，顺利得出结果。设小明购买故事书x本，购买漫画书ｙ本，则60x＋70ｙ≤500，（3≤x，2≤ｙ），因此，可以在直角坐标系中作出x＝3，ｙ＝2，ｙ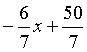＝图像，三条直线的交点坐标分别为：Ａ（6，2）、Ｂ（3，32/7）、Ｃ（3，2），则符合条件的组合就是三角形ＡＢＣ内的整数坐标点，通过图形可以直接得出（3，2）、（3，3）、（3，4）、（4，2）、（4，3）、（5，2）、（6，2），因此符合条件的组合一共有7种。通过数形转化，将学生的购买方式以坐标的形式呈现，降低了复杂的计算过程，提高了解题效率。

（四）直接转化，化具体现象为数学问题

数学核心素养下，教师在开展课堂教学时，应培养和发展学生的数学转化意识。借助数学语言描述问题，并运用数学方法解决问题的过程。可以说，在数学学习中，数学语言转化是数学学科与实际生活之间的纽带，也是提升学生数学应用能力的关键途径。因此，初中数学教师必须要在课堂教学中适当融入实际生活问题，指导学生运用所学的数学知识分析问题、构建数学模型、解决问题，最终在学习中促进数学探究能力的提升。例如，在《勾股定律》的教学中，教师在强化学生数学语言转化时，给学生融入了实际性的生活问题，某一个冷饮店中设计了一种饮料杯子，杯子呈圆柱性，内部地面的直径为5cm，高为12cm，当吸管放进杯中，吸管倾斜，顶端则会抵在杯子的边缘处，经过测量，杯口的外面漏出了5cm的吸管正好合适。那么，这个杯子的吸管应设计多长？接着，教师指导学生在分析的过程中，在纸上画出示意图，将杯子底部直径、杯子高度、吸管构成一个直角三角形，最终将实际问题转化为数学问题，引导学生借助勾股定理对其进行解决。如此，学生在数学学习中不仅强化了自身的数学转化思想意识，也促使其在学习中，真正实现了数学知识的灵活运用。

结语

在初中数学教学中，转化思想是一种十分重要的思维方式，教师应当将转化思想贯彻到初中数学教学当中，从而实现学生解题能力的提升。这说明在解决问题时可以灵活运用转化思维，将原题目进行重新分析、综合、归类等活动后，再利用所学知识与已有经验加以比较并重新分析综合。初中数学教学是我国基础教育阶段的重要组成部分，在初中数学教学中融人转化思想可以有效提升学生的思维能力，并且还有助于学生将数学知识融会贯通，有利于提高学生的综合素养。

参考文献：

［1］刘丼慧．探析转化思想在初中数学解题中的应用［Ｊ］．数理化解题研究，2015（4）：7８7９．

［2］陈旺，谢蓉．转化思想在数学解题中的几个策略［Ｊ］．语数外学习（数学教育），2013（９）：133．