引言

所谓“母题”变式，就是将教材中出现的题目作为研究的“母题”,教师引导学生对其思考、变式及应用^[3],由此衍生出与之相关的各类系列题型,再让学生根据母题变式形成的题目进行训练.这种由母题为起始的从一向多的发散性数学研究，不仅能让学生做到真正的跳出题海，更能让学生感受到数学独特的魅力.本文就将从三个角度对教材母题变式在初中数学的应用与实践进行探究.

一、出示母题，追本溯源

母题 人教版九年级上册第47页第4题

抛物线y＝ax²+bx+c与x轴的公共点是（-1，0），（3，0），求这条抛物线的对称轴.

分析 根据抛物线的对称性和与x轴交点坐标即可求解，求解过程中渗透了数形结合及直观想象素养.

解法1 将（-1，0），（3，0）代入抛物线解析式，得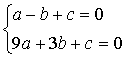，两式相减可消去c，得到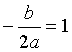，所以抛物线的对称轴是直线x=1.

解法2 ∵抛物线y＝ax²+bx+c与x轴的公共点是（-1，0），（3，0），

∴这条抛物线的对称轴为直线x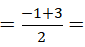1；

题后反思  考察抛物线与x轴的交点，以及如何求二次函数的对称轴，对于此类题目可将函数化为顶点式来求解也可以用公式法即x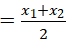求解，此方法更优，即抛物线y＝ax²+bx+c与x轴的交点是（x₁，0），（x₂，0），则抛物线的对称轴为直线x．

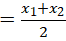二、灵活变换条件，探究新的结论—— 一题多变，逻辑训练

变式1 抛物线y＝ax²+bx+c，对称轴为直线x=1，且经过点（3，0），求与x轴的另一交点坐标.

变式2 抛物线y＝ax²+bx+c上部分点的横坐标x，纵坐标y的对应值如下表：

(1) 求抛物线的对称轴.

(2) 若A(-1，y₁)，B(-2，y₂)两点都在该函数的图象上，试比较y₁，y₂的大小.

变式3 抛物线y＝ax²+bx+c与x轴的公共点是（-1,0），（3，0），（0，-3）求这条抛物线的解析式.

总结 改变母题条件的呈现方式，根据抛物线相关点的特征进而推测函数的大致图象并结合抛物线的对称性，利用数形结合思想进行求解.

三、拓展题目模型，探究类似结论—— 一题多用，提升思维

变式4 二次函数y＝ax²+bx+c（a，b，c为常数）的部分图象如图①所示，设m=a-b+c，则m的取值范围是 　      　．

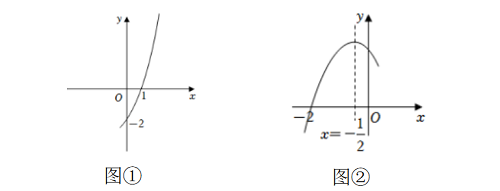
总结 二次函数往往由特征点得出解析式进而根据函数图象与性质解决相关问题，常常二次函数图象与系数的关系、二次函数与方程的关系、直角三角形勾股定理及其逆定理及三角形分类等知识综合，提升学生思维能力，利用数形结合思想，转化思想体现直观想象素养.

四、归纳母题出路，提高数学素养—— 一题多解，举一反三

变式7 如图③，抛物线y＝ax²+bx+3（a≠0）的对称轴为直线x＝-1，抛物线交x轴于A、C两点，与直线y＝x-1交于A、B两点，直线AB与抛物线的对称轴交于点E．

（1）求抛物线的解析式．

（2）点P在直线AB上方的抛物线上运动，若△ABP的面积最大，求此时点P的坐标．

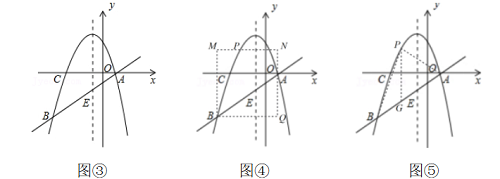
(1) 先确定出点A的坐标，根据抛物线的对称轴是直线x＝-1，求出点C的坐标，进而用待定系数法求出抛物线的解析式.

(2)解法1 设元补全图形求解法

先确定出点B的坐标，设点P（m，-m²-2m+3），见图④，利用S_△ABP＝S_矩形MNQB-S_△PNA-S_△PMB-S_△ABQ建立函数关系式即可得出结论.此法为学生初次解此类题易想之法，易于上手，但求解过程中运算较为繁琐，学生容易中途放弃，不推荐此法.

解法2 设元分割图形求解法

先确定出点B的坐标，设点P（m，-m²-2m+3），得出PG＝-m²-3m+4，见图⑤，利用S_△ABP＝S_△PGA+S_△PGB建立函数关系式时，学生难于表达分割后两三角形的高，根据x_A -x_P为△PGA的高，x_P-x_B为△PGB的高，我们易发现x_A -x_B为两三角形的高之和，即可顺利得出结论，此法为解此类题的通性通法.

解法3 平移直线切线法

先确定出点B的坐标，平移直线AB，设该直线l为y=x+b，使其经过点P，当直线l与抛物线只有一个交点此时△ABP的面积最大，直线与抛物线解析式联立方程组，根据二次函数与方程的关系中△=0求解出b，即可很快得出结论.

拓展 解法4 初高衔接求解法

先确定出点B的坐标，设点P（m，-m²-2m+3），求出直线AB的解析式，利用点到直线的距离公式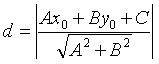，用含m的式子表达出△ABP的高的函数关系，因点A、点B为定点，即线段AB为定长，从而求解△ABP面积最大可转化为求解△ABP的高的最大值，此法对于学有余力的学生可适当拓展.适当也可渗透初高中衔接知识为有致于数学爱好者开一扇窗.

总结 此类最值题型为二次函数中较典型问题，在无法直接运用面积公式求解时，通常可采用割补法求面积，且分割图形法更优，若图形为三角形，则先求底边长和对应高，常以两轴上或平行两轴的边为底，以第三顶点的横或纵坐标的绝对值为其对应的高.常常也结合函数与方程、数形结合思想，直观想象素养并进行相应运算求解.

结语

于学生而言，从母题入手，灵活转换条件，拓展题目模型，归纳母题出路，与学生一起发散思维，不断向不同方向延伸，有效控制题量，从而使学生在学习数学时既能快速建立数学模型，又能提升学习数学的幸福感和参与感，形成良性循环.综合“母题”变式教学，有时会更切合实际，比进入题海更有效，更能提高学生训练的积极性.于教师而言，任何一堂课都要体现教师的主导作用和学生的主体地位，“母题”变式教学，教师俨然是教学的组织者和引导者，而不是“主宰”，虽然讨论的问题是教师引发的，但问题的进展是由学生决定的，这种把学习的主动权交还给学生的教学模式^[3]，能使课堂气氛和谐，师生关系融洽，从而达到更好的教学效果.

参考文献

[1]曾凯.以旧“唤”新,品味轴对称——一道教材母题的思考、变式及拓展应用[J].基础教育论坛,2017(13):50-51.

[2]李贵平.初中数学课本习题的变式与应用[J].宁德师范学院学报(自然科学版),2013,25(04):433-436.DOI:10.15911/j.cnki.35-1311/n.2013.04.027.

[3]王敏.一堂数学“母题”变式教学课的实录与感悟[J].数学教学通讯,2020(15):27-28.